How it is impossible to model reality, and how we will always be faking it.
Programmers and game designers sometimes start out a project with the noble intention of making the most realistic game possible. But as they progress, they discover that their initial dreams of realism are somewhat difficult to implement in a practical manner. Firstly, in the area of player control, the most realistic physics is often not the most enjoyable physics. Secondly, in the area of non-interactive effects such as explosions, smoke, etc, the programmer quickly finds that trying to accurately simulate the underlying physics is computationally infeasible.
This article discusses the problems of simulating reality, with particular reference to shattering glass.
INVESTIGATING REALITY
Shattering glass is used in many games. The most obvious use is a glass windows in shooters, where the player can shoot the window, leaving either a bullet hole, or shattering the whole window. But it is also used in other types of game where increased realism can benefit the game. In racing games, the car windows and headlights shatter in a crash. In basketball, the backboards sometimes shatter. Even in wrestling, a realistic looking fluorescent glass tube being smashed over your opponent’s head, can add to the feeling of immersion.
Suppose you, the programmer, have been tasked with making the glass shattering effect, and your producer has told you to make it “as real as possible” , how should you proceed? Well, perhaps the first thing you’d do is go and read some physics books, and do some searches on the internet, and try to find some physical models, some equations, that describe how glass shatters in the real world.
The first problem that you run across when trying to implement a “real” physical effect such as shattering glass, is that for a lot of these effects, nobody actually knows how they work in the real world.
Take another common effect: simulating fire. Nobody knows how the underlying physics of fire really works. Something as simple as a candle burning is a complex interplay of molecules, gravity, chemical reactions, and the heating, motion and radiation of multiple gases, liquids, solids and plasma. Since physics has yet to explain exactly what is going on when something burns; rendering an accurate image of the candle is an inexact task, involving light emitted from the burning gasses, reflected off the wick and the wax (both liquid and solid), transmitted and scattered through the solid wax, refracted through the pooled liquid wax, refracted through waves of rising hot air and vaporized paraffin, absorbed and reflected off the smoke particles and interacting with the rest of the environment. And that’s just for one candle, imagine if you had a whole cathedral full of them.
Similarly, scientists simply do not know how glass shatters. There are competing models of what is going on when a piece of glass breaks into two pieces. The debate is whether the fractures happen via the breaking of sub atomic bonds one after the other in the direction of the fracture, or if the fracture follows the formation of microscopic cavities that form ahead of the fracture tip. [1]
Unfortunately, while interesting, these distinctions are entirely academic to the game programmer. If you’ve gone as far as discovering this in your research, then you’ve probably gone too far, some things can never be simulated.
LIMITS TO COMPUTATON
The real world operates at a much finer grained level then is possible to simulate on a computer. The “real world” operates at the molecular, atomic and sub-atomic level. The so called “rigid bodies” that modern physics engines simulate are actually composed of septillions (1 septillion = 1 billion billion billion billion) of molecules, and it is the interactions between these molecules that create the apparent motion of the rigid body. In addition the time-step (or “main loop” ) of the real world operates in an essentially infinitely small step of time, compared with the 1/60th of a second that many game physics systems run at.
In last month’s article, I described simulating a “blob” with a mass-spring system. In the real world solid matter actually works a little like my blob, except that there are vastly more masses (molecules), an additional order of magnitude more springs (inter-atomic and inter-molecular forces), and a significant number of the springs keep breaking and re-forming.
So, if we want to simulate something as straightforward as a bullet going through a glass window, with the aim of it looking realistic, then what we can’t do is simulate the interactions of the 10^28 silicon molecules, with quintillions of simultaneous micro-fractures resolving into the macro fracture pattern we want.
Glass contains a lot of molecules. The most accurate simulation would simulation the state of each molecule, and the interactions between molecules. Even forgetting that we don’t actually know what is going on at the molecular level. The sheer number of molecules in matter is infeasibly huge. In a single gram of a material like glass, there are approximately 10^25 molecules. Even ignoring the physical limits of computing, Moore’s law will still require about 100 years before we’ll have enough computing power to even store the state of the simulation.
Still, much research has been done into precisely that type of simulation, albeit on a greatly reduced scale. It is still possible to simulate what is happening within a material using a molecular model, simply by making the molecules a lot bigger, so you don’t have to use as many of them. Results seem to be very realistic, but are still rather expensive. In 2002 ,the ASCII White, 12 teraflop, $110 Million, supercomputer ran simulations of fractures in a small cube of material with 1,000,000,000 (one billion) molecules, taking nearly two seconds per frame [2]. By comparison, the Sony PS3 has a theoretical performance of two teraflops, and it needs to do a lot more than simulate one crack.
So this hyper-realistic style of simulation is not yet feasible for video games. Hence we must move on to looking at models of the interplay of forces within the object that are much cheaper to implement. Realism must begin to take a back seat to another type of realism – the reality of our limited resources.
PRACTICAL SHATTERING
How quick does the shattering code actually have to be? Well, there are two main performance problems with shattering.
Firstly, shattering happens very fast. Cracks propagate in a material at about the speed of sound in that material. For glass, that’s around 5000 m/s. If simulating at 60 fps, then that means that any shattering of glass is effectively instantaneous. This then means that the entire calculation has to happen in a single frame.
Secondly, the shattering of an object turns what was a single piece of the environment, or a single rigid object, into hundreds of individual rigid objects, each requiring memory and CPU resources. If the player is given the freedom to shatter everything in sight, then how do we stop them exhausting system resources? Even in older games where the fragments vanished after a period of time, a common trick of games testers was to try to crash the game by shattering multiple objects at the same time, especially in split-screen mode.
What to do about the fragments generated is a problem with multiple solutions. You can devote a very large amount of your resources to these chunks (assuming it’s beneficial to the game somehow). You can make the chunks vanish after a period of time, or remove old chunks as new ones are generated, perhaps with some priority system. That’s more of a game design issue than a programming issue.
The problem of the time used in the generation of these chunks or fragments is another matter. If the shattering takes a long time, it can cause the game to glitch perceptibly. Players will be familiar with many games that slow down when a large amount of things are blown up. This can be due to an excessive amount of graphical effects on screen, but in more recent games this can also be due to increased physics complexity in the arena. Adding accurate shattering to the mix has the potential to greatly increase the amount of slow-down in such situations.
In order for the game not to slow down perceptibly, the shattering code must be able to shatter several objects per frame. Let’s say we can share the shattering over a few frames if we happen to have a large number of objects shatter simultaneously. Then a reasonable number would be perhaps ten objects shattered per frame, which must incur no additional overhead to the frame’s processing load. This essentially means we have to have some processing power kept permanently in reserve for this kind of thing. You’d probably not want to budget more than 10% of your processing for such frivolity as shattering objects, so that means each individual shatter must happen in less than 1% of a frame, or about 0.16 microseconds.
We can look at this another way. Assuming that the shattering effect is going to create a large number of rigid bodies that were not there before, then the system is going to have to be able to simulate and render those bodies without dropping speed. So all we have to do is to make it so that the shattering code for an object does not take longer than the simulation and rendering code for the rigid bodies that are generated by that shattering. However, this might not be true if the shattering of the object and simulation of resultant rigid bodies use different resource – such as when the shattering happens on the main CPU, and the simulation is on another processor such as the SPU, PPU or GPU.
BEYOND MOLECULES
The next step is to try to model the physical forces acting on an object at an event higher level, using something like a mass-spring system. We can devolve the object into a system of connected points as a mesh of triangles (or tetrahedrons), and then model the propagation of forces through this mesh, and allow object to split along lines or planes when the forces at that junction surpass a certain level.
Even a highly abstract simulation of shattering can be very time consuming. At the Game Developers Conference in 2002, O’Brian and Hodgins presented a method of 3D shattering using this kind of decomposition into tetrahedrons [3]. Their example of a single small wall took an average of 399 minutes to calculate a simulation of one second of shattering, based on 1999 hardware. Updated by a factor for twenty to 2006 hardware, this still only gives us about 1/1000th the speed of a real time simulation.
BEYOND PHYSICS
The problem with simulating physics is that, while we know what result we want to get, the physics model does not always supply this result, and it takes a long time to not supply it.
Instead, we can try to shatter glass based on purely aesthetic concerns. We can observe how glass breaks, and then try to duplicate it with simple heuristics.
Kadono and Arakawa used high speed cameras to study crack formation in a sheet of glass [4]. Other people have observed some consistent things about the way glass breaks when impacted by a small objects. Observations generally indicate the following simple rules:
1) Radial cracks propagate from the impact point like spokes on a wheel.
2) Other cracks propagate between radial cracks, like a spider web.
3) Cracks stop when they hit each another crack
4) The size of the glass fragments is a power function of the distance from the impact point.
These observations suggest a number of simple algorithms we could try. Since we are essentially generating a visual pattern, no physics need be involved, and we can use a number of “cheats” to get the result we want. In this case we can essentially generate the “spider web” pattern by:
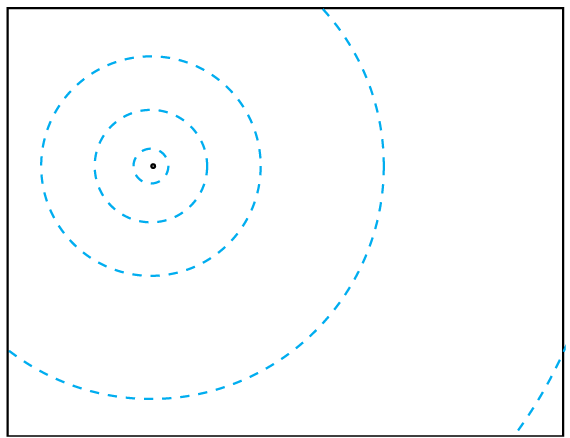
1) Imagine a framework of concentric circles, centered on the impact point, with the distance between them increasing exponentially. (figure 1)
2) Create jagged radial cracks by joining roughly equally spaced points on these circles in sequence from the center to the edge. (figure 2)
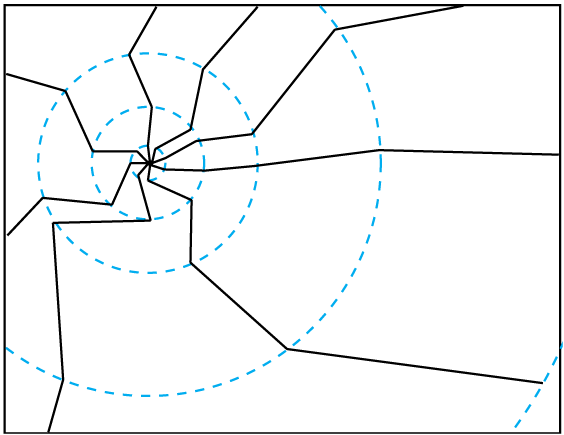
3) Create traverse cracks by joining sequential points on the circles (figure 3)

4) Turn the resultant quads into triangles by randomly splitting them along either diagonal. (figure 4)
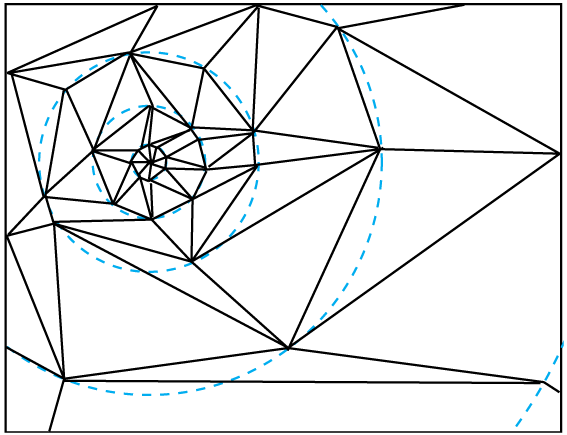
Now that’s a very simple algorithm, and it’s very fast. It will even give you a reasonable result for some types of glass and some type of impact.
There is lots you can do to extend it. You can add various types of random perturbation to make it look less regular. You can randomly join together adjacent triangles to create jagged irregular pieces (figure 5). You can let the radial cracks bifurcate. You could either arrange the line generation so there is no possibility of the cracks crossing (by limiting them to a angular segment), or you could allow your cracks total freedom, and have an additional step to detect and resolve crack-crack collision.
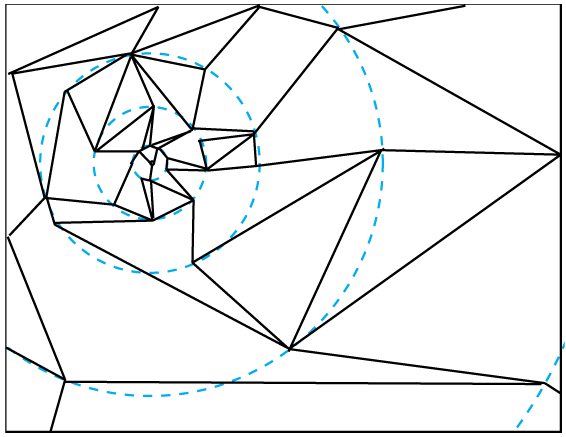
SUMMARY
Simulating the underlying physics of something that is essentially a cosmetic effect is often inefficient and does not always give satisfactory results. Simulating at any kind of molecular level is infeasible. Simulating as a system of joins and forces can give reasonable results, and much work is being done in this direction. However, you can still get a perfectly usable result by simply observing what is going on, describing it, and then simulating your description, without any need for understanding the underlying physics. Since your model is based purely on the visual results, it has the potential to look more aesthetically pleasing than a physics based solution.
References:
[1] Mills, W. What Makes Glass Break?, Research Penn State Magazine, October 31, 2005, http://www.rps.psu.edu/probing/glass.html
[2] Abraham, F. Simulating materials failure by using up to one billion atoms and the world’s fastest computer: Work-hardening , Proc Natl Acad Sci U S A. 2002 Apr 30;99(9):5783-5787. http://www.pnas.org/cgi/content/full/99/9/5783
[3] O’Brien, J. F., & Hodgins, J. K. (1999). Graphical Modeling and Animation of Brittle Fracture. ACM SIGGRAPH 99 (pp. 137-146). Los Angeles, California: ACM. http://www.cs.berkeley.edu/b-cam/Papers/obrien-1999-GMA.pdf
[4] Kadono, T, & Arakawa, M, Crack propagation in thin glass plates caused by high velocity impact, APS Physics Review, March 2002.
[…] programming reasons why we don’t shatter glass […]
Pingback by Welcome to Chris World! » ‘Text’ Editor — July 13, 2008 @ 1:15 am
http://propagandamatrix.com/forum/Packages/furniture/0/wicks-furniture-store.html wicks furniture store http://propagandamatrix.com/forum/Packages/furniture/0/wicks-furniture.html wicks furniture http://propagandamatrix.com/forum/Packages/furniture/0/wickesfurniture.html wickesfurniture
Comment by wicks furniture store — August 26, 2008 @ 5:52 am
I couldn’t find any good pictures or youtube videos, but Counter Strike Source has awesome glass breaking, the office level specifically. Glass is transparent to start with, then you shoot a bullet in one corner and a hole is blown out of the glass where it hit and around it are the spider web cracks like you described. Then you can walk through the glass window and only the parts that walk through are knocked out, so it is must be divided into a 2d grid or something. Anyway, it’s pretty cool, you’ve probably seen it before.
Comment by Chris — February 22, 2009 @ 1:28 pm
great page! thanks
Comment by lazer epilasyon — April 2, 2009 @ 2:37 pm
Ya know, for the last couple generations, it seems people say “By the time YOU grow up….” But I really don’t see this happening in the next few generations either.
Comment by software gestionale — November 2, 2009 @ 10:41 am